4212. Кастинг

В театре работает n актеров. Известно, что среди них a высоких, b голубоглазых и с блондинов. Для главной роли в новом спектакле режиссеру требуется только один высокий голубоглазый блондин. Чтобы спланировать свое время для беседы с каждым таким артистом из труппы театра, режиссеру необходимо узнать, какое максимальное или какое минимальное количество артистов из работающих в театре подходит для этой роли.

Требуется написать программу, которая по заданным числам n, a, b и с определяет минимальное или максимальное количество актеров, с которыми режиссер должен переговорить.

Вход. Первая строка содержит одно число, которое задает, минимальное или максимальное количество актеров необходимо найти в данном тесте. Это число может принимать следующие значения:

· 1, если в данном тесте требуется определить минимальное количество актеров;

· 2, если в данном тесте требуется определить максимальное количество актеров.

Вторая строка содержит четыре целых числа: n, a, b, с (1 ≤ n ≤ 10000, 0 ≤ a, b, c ≤ n).

Выход. Вывести одно число – минимальное или максимальное (в зависимости от входных данных) количество актеров, которые могут претендовать на главную роль в новом спектакле.

Пример входа 1	Пример выхода 1
2 5 3 4 5	3
Пример входа 2	Пример выхода 2
1 5 3 4 5	2

РЕШЕНИЕ

математика

Анализ алгоритма

Максимальное количество актеров будет, если стараться присваивать людям максимальное количество свойств. То есть берем первого человека и присваиваем ему все три свойства. Если еще имеются в наличии все три свойства – присваиваем их второму человеку и так далее. Действуя подобным образом, мы получим что максимальное количество актеров которым одновременно можно присвоить все три свойства, равно min(a, b, c).

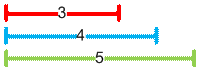
Для поиска минимального количество актеров сначала упростим задачу: предположим, что у нас имеются только два, а не три параметра – например a и b. Если a + b ≤ n, то среди n актеров a могут быть высокие, и b голубоглазые, причем ни один из актеров может не обладать одновременно двумя указанными свойствами. Выстроим актеров в круг. Первым a (актерам с номерами от 1 до a) назначим свойство “высокий”, следующим b по кругу (начиная с номера a + 1) назначим свойство “голубоглазый”. Если a + b > n, то оба свойства присвоятся актерам с номерами 1, 2, … . При таком назначении свойств мы получим минимальное пересечение по свойствам, которое равно a + b – n при a + b > n) или 0 если a + b ≤ n.

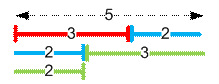
В случае трех параметров также расставим актеров в круг. И будем назначать им свойства по кругу. Тогда минимальное количество актеров, которое будет обладать всеми тремя свойствами, равно max(a + b + c – 2n, 0).

Реализация алгоритма

Читаем входные данные.

scanf("%d %d %d %d %d",&type,&n,&a,&b,&c);

if (type == 1)

{

Вычисляем минимальное количество актеров.

res = a + b + c - 2 * n;

if (res < 0) res = 0;

}

else

{

Вычисляем максимальное количество актеров.

res = min(a,b);

res = min(res,c);

}

Выводим ответ.

printf("%d\n",res);